对单子的求索
如是我闻:
单子空空,力量无限
用之愈多,所得愈多
谈之愈多,知之愈少
——《单子之道》
这样说不知是否夸张,似乎每个懂得了单子的程序员都会写一篇关于它的文章(而且每一篇的开头都是:网络上已经有了许多单子指南,但是……)。原因是对于单子的理解像是一种灵魂感悟,你想与他人分享。
人们对单子的认知如同盲人摸象。你会看到有的人将它描述为容器,有的人将它描述为动作。有的人认为它是用于封装副作用的,也有人将其视为范畴论中自函子的实例。
很难说清楚单子是个什么东西,因为它与我们日常生活中的事物毫无关系。对于面向对象编程中的对象,即使婴儿都知道对象是什么(可以放进嘴里的东西),单子该如何具化?
第一部分
还是让我们首先回答一个相关的问题:
单子为何这么二?
单子使得纯函数式程序员能够实现变量、状态、I/O 以及其他那些并非函数的东西。嗯,那你可能要说了,他们活该啊……他们将手绑在身后,吹牛说他们可以用脚趾头打字。就让他们作吧,我们没必要关心。
事实上,我们在命令式语言中经常使用的那些非函数式的东西是诸恶之源。以副作用为例,聪明的程序员(可理解为手指多次被烧的家伙)出于对副作用的畏 惧而倾力消减全局变量与静态变量的使用。如果你知道你在干什么,这样是切实可行的。但是游戏规则的真正篡改者是多线程。线程共享状态的控制已经逾越了优秀 的编程经验的界限,成为了一项必备的生存技能。一些极端的编程模型已经完全的消除了共享机制,像 Erlang 那样完全的进程隔离,并将消息传递限制为值传递。
单子在完全无政府主义的命令式语言与孤立主义的类 Erlang 语言之间的地带扎根。单子不禁止共享或副作用,而是让你去控制它们。并且由于这种控制是通过类型系统来运作的,因此使用单子的程序可由编译器来检测其正确 性。想想命令式程序中数据竞争测试的难度,我认为花点时间学习一下单子是值得的。
也有一个完全不同的概念:元编程。C++ 元编程中所用的模板语言是一种纯函数式语言(见我的博文,Haskell 与 C++ 的关系)。如果单子在函数式编程中非常重要,那么在 C++ 元编程中也必会如此。事实的确如此。我打算在以后的文章中来讨论这个问题。
现在,我们开始探索单子究竟是个什么东西。
范畴论中的答案
如果你不知道范畴论,也不必担心。它其实是相当简单的概念,可以描述许多事物,而且你还能从中赚取一些吹牛的资本。我的主要目标是分享一些数学上的 直觉。这部分内容,我会解释范畴、函子、自函子,以它们为基础进而解释单子。我会给出来自日常生活与编程中的一些的实例。我会在下一部分真正的讲述单子及 其实际应用,因此请耐心一些。
范畴
范畴是集合与函数概念的自然扩展。泛化了的集合在范畴中被称为对象(一个稍微有些实际语意相当中性的词语),泛化了的函数被称为态射。实际上,范畴的标准实例是一个集合与函数构成的范畴,称为集合范畴。
一个态射(可理解为“函数”)从一个对象(可理解为“集合”)到另一个对象。数学函数,例如 sin 或 exp,通常是从一个实数集到另一个实数集的。但是你也可以定义 isPrime 这样的函数,从自然数集到布尔数集,或者定义一个 price 函数,从货物集到数集。
对于态射,只需知道它们可被复合即可。对于从 A 到 B 的一个态射,A->B,还有一个从 B 到 C 的态射,B->C,那么它们可复合维一个从 A 到 C 的态射,A->C。就像函数的标准复合那样,态射复合也必须满足结合律,这样在复合多于两个态射时,我们就可以省去一些括号了。
实际上,我们还需要知道一件事。对于每个对象,有一种特定的态射称为 identity(单位态射),它什么也不做,当它与其他态射复合时会产生与后者相同的态射。
说点题外话,范畴不一定非要建立于集合与函数之上。通过圆圈与箭头就可以很容易构建出简单的范畴。图 1 显示了一个包含两个对象(圆圈)与四个态射(箭头),可以看出任意两个态射都可以复合,而且 iA 与 iB 是单位态射。
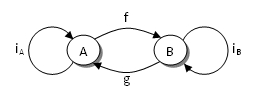
就这么多了。希望我已经使你深信范畴并不是什么了不起的东西。但是,我们还是务实一些。在编程语言中一个真正重要的范畴就是类型与函数的范畴,在 Haskell 中它被称为 Hask 范畴。一般是有一个基本类型的有限集,例如整型、布尔类型等;还有一个派生类型的无限集,像整型列表,从整型到布尔类型的函数等。在 Hask 中,类型仅仅是值的集合。例如 Char 类型是 {‘a’, ‘b’, ‘c’, …} 集合。
因此,在 Hask 范畴中,类型是对象,函数是态射。实际上,函数将一种类型映射为另一种类型(暂时忘掉多个参数的函数——它们可以被柯里化构建为单参数函数——和多态函数 ——它们是函数族)。并且在函数式编程观念中,这些函数如果给它们同样的值,它们也会返回同样的结果——没有副作用。
函数复合不过是将一个函数作为另一个函数的参数而已。单位函数接受 x 然后立刻将其返回。
这些都还好理解,但是有什么用呢?也许你会问。那么我们就来进行第一次洞察和顿悟吧。如果有一种你称之为编程本质的东西,它就是可复合性。在任何编 程风格中,你总是会将一些小块复合起来构建你的程序,这些小块又来自更小的块的复合。这就是具有可复合态射的范畴之所以如此重要的原因。乐高积木的本质就 在于它们的适配性、可组合性,而非颜色与尺寸。函数式编程的本质就是函数如何协同工作:如何通过小的函数来构建大的函数。
每个范畴都是由它所选择的对象和态射来定义的。但是否有一种方法可以描述某个给定的范畴,并且这种描述独立于范畴所选的特定的对象与态射?即如何展 现一个特定范畴的内部结构?数学家们肯定知道怎么做。你需要将范畴映射为其他范畴,同时保留对象之间的态射以及态射的复合方式。这样的映射可以让你发现范 畴之间的相似性并对不同种类的范畴进行编排。至此,事情才真正变得有趣起来。
函子
函子 F 是一个范畴到另一个范畴的映射:它将对象映射为对象,将态射映射为态射。但是函子不能随意胡为,因为这样会破坏我们所追求的结构。因此我们必须要施加一些明确的(数学家喜欢这个词)约束。
首先,如果你在第一个范畴中两个对象之间有一个态射,它被很好的映射为第二个范畴中两个对象的之间的态射。如图 2 所示,对象 A 被映射为 F(A),对象 B 被映射为 F(B)。从 A 到 B 的态射 f 被映射为从 F(A) 到 F(B) 的态射 F(f)。数学家说像这样的图必须满足交换律,就是说无论是先将 A 映射为 F(A) 然后应用 F(f),还是先应用 f 然后将 B 映射为 F(B),结果必须相同。

图 2. 作用于对象 A 与 B 及态射 f 的函子 F。底部是 F 的域(源)范畴,上部是它的陪域(目标)范畴
还有,这样的映射应当保留态射的复合性。因此如果态射 h 是 f 与 g 的复合,那么 F(h) 必定是 F(f) 与 F(g) 的复合。当然,函子也必须将单位态射映射为单位态射。
为了感知函子是如何被这些条件约束的,想象一下如何将图 1 中的范畴映射为其自身(像这样的函子只是重新安排了一个范畴内部的东西)。有两种简单的映射可将两个对象折叠为一个(要么是 A,要么是 B),并将所有态射转化为单位态射。还有一种单位函子,可将两个对象映射为其自身,也可将所有态射映射为其自身。最后,还有一种有趣的函子,它可将 A 映射为 B,将 B 映射为 A,将 f 与 g 的功能对换。现在想像一下有一种与图 1 相似的范畴,只是去掉了态射 g(是的,这仍然是一个范畴)。这一下图 1 所示的范畴与这个新范畴之间除了折叠函子之外,其他函子都不存在了。这是因为这两个范畴有着完全不同的结构。
现在我们进入更加熟悉的领域。因为我们主要是对 Hask 这种范畴感兴趣,那么我们就定义一个函子,将这个范畴映射为其自身(像这样的函子称为自函子)。Hask 中的一个对象就是一个类型,因此我们的函子必须将类型映射为类型。这种方式看上去就像是 Hask 中的函子可以从一种类型构建出另一种类型——它就是一个类型构造子。不要被名字搞晕了:类型构造子在你的程序中创建新类型,但是那种类型是已经存在于 Hask 范畴之中。
以列表类型构造子为例。对于给定的任何类型,列表构造子都可以构建出这种类型的列表。整型类型 Integer 被映射为整型列表,用 Haskell 的行话来说,就是 [Integer]。注意这并非是定义在整型数值,例如 1, 2 或 3 之上的映射。它也不会在 Hask 范畴中增加一种新的类型——[Integer] 已经存在于 Hask 范畴之中。它只是将一种类型映射为另一种类型而已。对于 C++ 程序员而言:可以思考一下类型 T 与 T 的容器之间的映射,例如 std::vector。
类型的映射比较容易,对于函数该当如何?我们必须寻找一种方式,可以接受一个特定的函数并将其映射为一个操作列表的函数。这也很容易:将这个函数依 次作用于列表中每个元素即可。Haskell 中有一种(高层)函数可以做到这一点。这种函数被称为 map,它接受一个函数和一个列表,然后返回一个新的列表(或者由于柯里化,你可以说它接受了一个函数并返回一个可以操作列表的函数)。在 C++ 中,有一种类似的模板函数,std::transform(嗯,它接受两个迭代器和一个函数对象,不过思想是相同的)。
数学家通常使用图形来表示态射与函子的性质(如图 2).用于表示态射的箭头通常是水平的,用于表示函子的箭头通常是竖直的(向上的)。这就是为什么函子对态射的映射通常被称为提升。你可以接受一个操作整型数的函数,然后将其提升为一个操作整型列表的函数,等等。
列表函子显然保持了函数的复合性与单位性(这个要留给读者当作一个简单但有意义的课后作业)。
现在来进行第二次顿悟。编程的第二个本质是什么?复用性!来看我们是如何做到的:我们接受已经实现的所有函数,然后将其提升为列表级别的函数。我们 得到列表操作函数基本上是免费的(好吧,我们得到的是那些函数的一个很小但是非常重要的子集)。同样的技巧可用于所有类型的容器,数组、树、队列、智能指 针等等。
这一切都非常优美,而且你不需要懂范畴论就可以应用这些函数处理列表。在编程中能够发现模式总是好事情,而这个则是模式的管理者。真正的革命始于单子。猜猜原因是什么?列表函子实际上是单子。单子相对于函子,只不过配料更多而已。
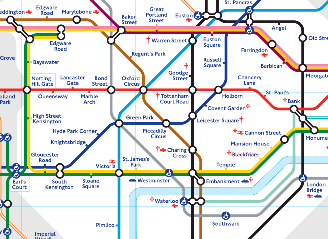
这种通过映射来暴露系统结构的描述背后的直觉是什么?思考如图 3 所示的伦敦地铁路线图。该图只是由许多圆圈与线段构成。但它们是有意义的,因为伦敦城与这副图之间存在着映射。圆圈与地铁站相关,线段与铁路线相关。更为 重要的是,如果列车在两个站点之间运行,那么图中相应的圆圈可以用线段连接起来,反之亦然:这些就是映射所保持的约束。地铁路线图显示了一种存在于伦敦 (地下)的一种特定的结构,通过映射的方式使之昭然若揭。
图 3. 伦敦地铁路线图有趣的是,我在此所做的也是映射:伦敦与地铁路线图对应着两个范畴。地铁站/圆圈是对象,地铁线路/线段是态射。这个例子如何?
自函子
数学家喜欢可以保持明确约束的映射。正如我所解释过的,这样的映射从实现的细节中抽象出内部结构。但是你也能够通过研究自我映射的方式对结构有更多 的了解。将一个范畴映射为其自身的函子称为自函子(像是可让你看见内部事物的内窥镜)。如果说函子揭示了范畴之间的相似性,那么自函子就是揭示了范畴的自 相似性。观察一下图 4 所示的分形蕨类,你就会明白自相似性多么强大。

图 4. 由 4 个自态射构造的分型蕨类
稍微想像一下,你就会看到列表函子揭示了 Hask 范畴中像蕨类那样的结构,如图 5 所示。一组 Char 类型构成 Char 列表,一组 Char 列表又构成 Char 列表的列表,诸如此类,无穷无尽。由 Char 到 Bool 的函数所描述的水平结构被提升到高而更高的层次,使之作用于列表、列表的列表等等。
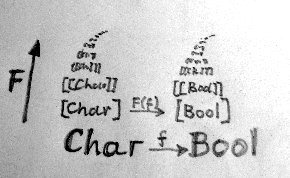
图 5. 列表类型构造子的行为揭示了 Hask 内部类似蕨类的结构。这个函子将各个函数提升了,函数作用于水平方向
可将接受类型参数的 C++ 模板视为类型构造子。用它来定义一个函子怎么样?(不严格的说——C++ 不像 Haskll 那样数学化)。你必须自问:类型参数是被以任意方式约束的么?通常会很难回答,因为类型约束是隐藏于具体模板中的,只有在初始化期间方可测试。例 如,std::vector 的类型参数必须是可复制的。这样的话就排除了具有私有成员或者删除了 copy 构造函数的类。不过这没什么问题,因为可复制的类型形成了一个子范畴(相当不严格的说)。重要的是一个可复制的向量其本身是可复制的,因此态射的“自”的 部分就有了。通常你会希望能够将类型构造子所创建的类型再喂给这个类型构造子,就像这样 std::vector<std::vector>。当然,你也必须能够以一种一般化的方式提升函数,就像 std::transform 那样。
单子
呃,单子。
—— Haskell Simpson
终于到了揭开面纱的时刻了。我将会从单子的定义开始,其定义建立于前几节内容之上并且被数学家们广为使用。还有一个不那么直观但是更容易在编程中使用的定义,我会放在后面讲。
单子是一个自函子,伴随两种竖直方向特定的态射族,一种是向上的,一种是向下的(对于方向,参考图 5)。向上的那种态射被称为 unit,向下的那种被称为 join。
现在我们已经见识了太多的映射魔法,因此还是放慢脚步去构建一些直觉。记住,函子映射了对象:在我们的例子中,类型是值的集合。函子不会去看对象内 部是什么,这个事情通常是态射做的。在我们的例子中,态射是将一种类型的值映射为另一种类型的值的函数。我们的函子是通过类型构造子定义的,通常是将一种 穷类型映射为富类型,例如 Bool 类型是两个值的集合,而 [Bool] 是两个值所构成的无穷无尽的列表集合。
unit 态射接受一种穷类型的值,然后选一个富类型的值,然后宣称它们大致等价。Bool 对象的 True 值的一个大致等价是 [Bool] 对象的一个单元素列表 [True]。类似,unit 将 False 映射为 [False]。它也可以将 5 映射为 [5] 等等。
可将 unit 视为将一个底层的值嵌入到高层的一种自然的方式。顺便说一下,在编程中,那些为任意类型而定义的函数族被称为多态函数。在 C++ 中,我们可将 unit 表示为模板,像这样:
1 2 3 4 5 6 |
|
为了更好的解释 join 态射,想象一下作用两次的函子。例如,对于一个给定的类型 T,列表函子会首先构造类型 [T],然后构造 [[T]]。join 态射会通过子列表的合并而移除一层列表态。通俗的说,它只是将内部列表连接起来。例如,给定的 [[a, b], [c], [d, e]],join 态射会将其映射为 [a, b, c, d , e]。它是从富类型到穷类型的多向到单向的映射。join 态射的类型参数化也会形成一个多态函数(C++ 中的模板)。
有几条单子定律定义了 unit 与 join 的性质(例如 unit 与 join 彼此对立),但是我不打算对它们详加解释。unit 与 join 存在的重要意义是对自函子施加了新的约束,从而将范畴更多的内部结构刻画出来。
对于以 unit 为中性元的所有乘法而言,数学家将 join 视为其祖父。它对于数学家非常重要,因为乘法导出了代数结构,并且事实上单子对于代数的构建并发现其隐含的性质具有重要作用。
与数学家不同,我们这些程序员对于代数结构不感兴趣。因此一定有什么东西使得单子如此重要。正如我在开始时所讲,在编程中我们经常面临那些没法自然 转化为函数式范式的问题。有一些计算方式可以使用命令式语言很好的表示。这并不是说他们不能被转换为函数式,仅仅是这种转换有些笨拙和乏味而已。单子提供 了一种优雅的工具来实现这种转换。单子使得在函数式编程中吸收与同化命令式编程风格成为可能,以致许多人宣称(戏谑?)Haskell 是最好的命令式语言。像所有的东西一样,函数式的单子势必峰回路转,在命令式编程中找到它的位置。
第二部分
函数式编程面临的挑战
函数是什么,你懂的:每次以相同的参数调用它,它总是会返回同样的结果。大量有用的计算直接映射为函数,但依然有许多计算没法这样做。我们经常不得 不涉及一些非函数的计算方法。在非函数式语言中,这样的计算也经常被称为“函数”。Eugenio Moggi,这哥们将单子引入了计算,对于这样的“函数”给出了一些例子:
- 偏“函数”:永不截止的参数值(例如陷入了死循环)。这些并非数学意义上的函数。
- 非确定“函数”:它们不返回单个结果,而是返回多个可选的结果。非确定解析器类似这样。对于给定的输入,它们返回一个可能的解析结果的集合,这些解析结果都可能是正确的,具体选择需要依赖具体环境。这样的函数并非真正的函数,因为一个函数必须要返回单个值。
- 带副作用的“函数”:它们能够访问和修改外部状态,并且可被重复调用,每次都依赖于状态而返回不同的结果。
- 抛出异常的“函数”:它们并非是为特定的参数值(或状态)而定义,并且它们抛出异常而不是返回一个结果。
- 续延(Continuation)。
- 交互输入:getchar 是个很好的例子。它的结果依赖于键盘的敲击。
- 交互输出:putchar 是个很好的例子。因为它不能返回任何东西(如果它返回一个错误码,它就不依赖于参数值),所以它不是函数。还有,如果我们想将任何东西显示于屏幕上的时候,它便不能被优化掉。
奇异的事情是使用一些创造性的方法,这些问题是可以使用纯函数的方法来解决的。我不会讨论所有的问题,但是我会向你展示一系列渐进而有趣的例子。
错误传播与异常
所有人都要处理错误的传播。我们将问题剖开:你正在定义一种仅针对可能参数值的子集而返回有效结果的计算。如果参数值是“错误”的,那么这个函数会发生什么?嗯,你会让他返回一个错误。
最简单的情况下,你可能会向返回值增加一位,表示成功或者失败。有时你也可以在返回值类型中增加一位:如果结果正确,那么它就是非负的,否则就是错 误的。或者,如果返回值是指针,你可以返回一个空指针。但是这些办法只是为了效率而引入的一些小技巧。与大部分的小技巧一样,它们可能会导致危险的代码。 看下面的代码(不大正确):
1 2 |
|
如果 fileName 不包含点,结果是一个特定的值 npos,表示一个错误。问题是 npos 与非错误的结果并非同一类型,以致它在安静的传递给 string::substr 函数时导致一个未定义的行为。
一个更加通用并且安全的方案是更改——扩展——结果的类型,使之包含一个错误位。对于任何类型你都可以这样做。在 Haskell 中,你只需定义一个叫做 Maybe 的类型构造子即可:
1
|
|
它接受一个任意类型 a,然后定义一种新的类型,该类型为类型 a 的可能集合增加了一个特殊的值 Nothing。在 C++ 中,这种做法等价于这样的模板:
1 2 3 4 5 |
|
(这只是一个示例而已。并非是讨论在 C++ 中 Maybe 会非常有用,C++ 有它自己的错误传播机制。)
这样我们就有了一种可将一种没有针对所有的值而定义的函数转化为覆盖整个值域的函数了,只不过它返回的是一种新的富类型。
第二个问题是这些新东西——返回 Maybe 的函数——可以复合吗?当调用者本身是更大计算的一部分的时候,它该如何处理这种函数的结果?有一件事情可以确定,这种函数的结果不能被直接传递给一个不 对错误进行检测的函数——错误不能被轻易的忽略——即便这种函数很优秀。如果我们使用一个返回 Maybe 的新函数 safe_find 来替换 find 函数,用户不能使用 substr 来调用它。因为类型不匹配。相反,safe_find 的结果必须要被解开并且进行测试(与我们之前做的差不多)。
1 2 3 4 |
|
注意这里发生了什么:通过更改函数的返回值类型,我们打破了函数组合的自然方式——一个函数的结果是下一个函数的输入。但是从另一角度来看,我们已经对这些函数提出了一种新的复合方式。看我如何以更好的效果将函数组合起来的:
1 2 3 4 5 6 7 8 9 10 |
|
上面第 2、4、6 行代码就是胶水,用来复合我们的新的、更能容错的函数。注意这种模板式的胶水是如何以代码的形式直白呈现的。再完美一些,我们可能更喜欢像下面这样来写代码:
1 2 3 4 5 6 7 |
|
其中 DO 可以隐式的提供这样的胶水用来复合 f, g 与 h。
在 C++ 中要实现 DO 这样的胶水抽象会很难。我不打算折腾了。但是在 Haskell 中则别有一番天地。我们还是将上面的 C++ 代码翻译成 Haskell 代码:
1 2 3 4 5 6 7 8 9 10 11 |
|
C++ 代码中的 if 语言在 Haskell 中可以使用模式匹配(case x of)来替代。ms 是 Maybe 类型,ns 是 m 所包含的内容(假定 ms 不是 Nothing)。
注意代码中的级联格式特征——嵌套的条件语句或模式匹配。我们分析其中的一层。代码是从一个 Maybe 值开始的(f n 的结果),第一层胶水是第 3—5 行代码。我们将这个 Maybe 值打开并且检测其中的内容。如果结果并非错误(Just n1),就继续执行后面的函数复合代码,即 6—11 行代码。
如果结果是一个错误的话(模式匹配的 Nothing 分支),整个“剩余的复合代码”就会被忽略,这一点也非常重要。为了对胶水进行抽象,我们也必须对“剩余的复合代码”进行抽象。像这样的抽象,被称为“延 续体”(Continuation)。我们可将续延写为 lambda 函数(Haskell 中的 lambda 使用反斜线表示,就是希腊字母中的 λ 断了一条腿):
1 2 3 4 5 6 7 |
|
这里有个技巧:我们可以将胶水抽象为一个(高阶)函数,它接受一个 Maybe 值和一个续延。我们称这个新的函数为 bind,利用它重写 compose 函数如下:
1 2 3 4 5 6 7 8 9 10 |
|
bind 函数的实现如下:
1 2 3 4 |
|
或者更加紧凑一些:
1 2 |
|
图 6 展示了整个代码的变换。 f n 的结果是一个 Maybe 值,它被传递给采用蓝色盒子表示的 bind 函数,在 bind 内部,Maybe 值被解开,如果所得的值是 Nothing,那么就什么都不发生;如果值是 Just n1,剩余的代码,即续延会被使用 n1 作为参数值而调用。续延本身可以使用 bind 进行重写。最终的续延称为 return,后文再对它进行解释。
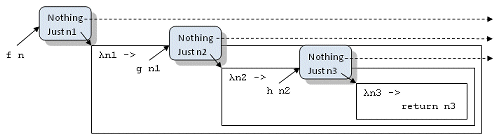
图 6. 返回 Maybe 值的函数的复合
图 6 中的蓝色盒子,bind 的位置在 Maybe 参数值与续延之间,这暗示这中缀表示可能会更合适。的确是这样,在 Haskell 中 bind 是使用中缀操作符 >>= 来表示的:
1 2 |
|
(等号的左侧是位于两个参数值【实际上是模式】之间的操作符,右侧是函数体)我们可以将这个 bind 函数的类型表示为:
1
|
|
它表示接受一个 Maybe a 和一个从 a 到 Maybe b 的函数(即我们的续延),然后返回一个 Maybe b。在处理高阶函数时,我发现类型签名尤为有用;因此我经常使用它们来株式我的 C++ 元代码。
使用 >>= 重写 compose 函数如下:
1 2 3 4 5 |
|
现在到了解释函数末尾那个神秘的 return 的时间了。它当然不是表示从函数中返回一个值那样的关键字。它是一个函数,接受一个类型为 a 的参数值然后将其转化为一个 Maybe a 值:
1
|
|
我们之所以需要 return 是因为 compose 的结果是一个 Maybe 值。如果 compose 中的任何一个函数都返回 Nothing,那么 compose 也会返回 Nothing(这是 >>= 的定义决定的)。只有在全部函数都成功的发生了作用之时,我们才应用 return 获得正确的结果 n3。return 将 n3 变为 Just n3,这宣示了计算是成功的,并且封装了最终的结果为 Maybe 类型的值。
你可能认为使用 return 而不是直接使用 Just n3 有点太折腾了,事实上这样做是有道理的。一个理由是可以将直接访问 Maybe 的实现隐含起来。另一个理由是这种方式适用于处理 Maybe 之外的其他情况。
Maybe 单子
Maybe 与单子有什么关系?可以从一个更加宽泛的视角来看前面我们做过的事情。
前面我们是从一种行为不太像函数的计算开始的——即它的定义并非针对全部的参数值。我们已经发现了一种聪明的方式,通过增强其返回值的类型而将其转化为函数。像这样的类型增强可以表示为类型构造子。
从范畴论的视角来看,定义一个类型构造子,实现从类型到类型的映射,这已经完成了自函子的一半工作。剩下的工作就是实现函数(态射)的映射。对于任 何可将类型 a 的值映射为类型 b 的值的函数,我们需要一个与之对应的函数,它可以作用于被增强的类型。在 Haskell 中,函数到函数的映射可以表示为高阶函数。如果这种映射是自函子的一部分,那么对应的高阶函数被称为 fmap。
假设我们有一个类型构造子 M,它可以构造类型 a 的增强类型 M a。函数 fmap 的签名可表示为:
1
|
|
它将一个从 a 到 b 的函数映射为从 M a 到 M b 的函数。对于 Maybe 而言,我们已经知道了它的类型构造子部分,关于它的 fmap 下面便会有讲。
让我们回到那个体现为返回一个增强类型的函数上,其类型签名一般为:
1
|
|
因为我们关注的是计算的复合性,我们需要一种方法可将这些增强的函数粘合到一起。在粘合的过程中,我们必须对增强类型的值进行检测并作出决断,例如 判断是否继续执行剩余的计算或者终止。因此具有一般性的 bind 操作必须接受两个参数值:之前的增强函数的结果与剩余计算——一个续延:
1
|
|
如果你足够斜眼的话,便可以发现 bind 与 fmap 之间的相似性。
可以这样认识 bind 与 fmap 之间的相似性:想像一下你向 bind 提供了第二个参数值,那个续延。这样便余下一个类型为 M a 的自由参数,从而便构成一个从 M a 到 M b 的函数(这个不是严格的柯里化,因为我们正在固定第二个参数值而不是第一个,但是思想是一致的)。这个从 M a 到 M b 的函数恰恰是 fmap 签名的右半部分。这样来看,bind 实际上是将函数映射为函数:
1
|
|
左侧的函数是一个续延,右侧的那个是 bind 协同第二个参数值(那个续延)所构成的函数。
因此 bind 函数的签名颇为类似 fmap,但是还不够。好在我们的装备种还有一个函数族,那个多态的 return。return 的签名是:
1
|
|
使用 bind 与 return,我们可以提升任何函数 f:
1
|
|
使之成为函数 g:
1
|
|
下面是一个通过 f, bind 与 return 定义函数 g 的魔幻公式:
1
|
|
使用中缀表示法可写为:
1
|
|
这种将 f 化为 g 的映射就是我们对 fmap 的定义。当然,fmap 必须服从一些定律,特别是它必须保持函数复合性以及与 unit 交互的正确性。这些定律主要体现为与 bind 和 return 相关的一些条件,在此我不打算讨论它们。
现在只要单子具有两个组成部分:unit 与 join,那么我们便可重现函子。显然 return 只是 unit 的化名,对于任意类型,它以最自然的方式将这种类型的值提升为一个富类型的值(顺便说一下,“自然”这个词在范畴论中有一个非常精确的意义;unit 与 join 都是函子 (M, fmap) 的自然变换)。
为了重现 join,先看一下在 Haskell 中它的类型签名:
1
|
|
它将类型构造子坍缩了一层。对于 Maybe 而言,它应当将双层 Maybe 映射为单层 Maybe,即它应当将 Just (Just x) 映射为 Just x,其他值都映射为 Nothing。其实有一种更加通用的方式来定义 join 函数,使用 bind 与单位函数即可实现:
1 2 |
|
我们所做的是将类型为 M (M a) 的值绑定到 id 函数。这个 id 函数作用于 M a 值,返回是相同的 M a 值。你完全可以确信这些类型签名是匹配 bind 的签名的(见附录);而且这个定义作用于 Maybe 时,会产生正确的结果。
总结一下:在这里我们所做的就是展现了具备 bind 与 return 的 Maybe 是范畴论意义中的单子。实际上,我们展现了更为一般的东西:由类型构造子与 bind、return 这两个服从一些定律的函数所构成的所有的三元组,每一个都定义了一个单子。在范畴论中,这个三元组被称为 Kleisli 三元组,可当作单子的另一种定义。
语法糖
现在你只是见识了 Maybe 的例子,可能看上去我们是拽出一只单子迫击炮灭掉一只蚊子。不过你以后会看到,披着不同伪装的同样的模式在大量的场合不断重现。实际上这在函数式语言中相 当普遍,因此需要构建的语法糖。在 Haskell 中,这种语法糖叫 do 表达式。让我们倒一下车,看看 compose 的实现:
1 2 3 4 5 |
|
下面是以 do 表达式写出的等价代码:
1 2 3 4 5 6 7 |
|
看上去伪装的很像一种命令式程序。下面是一个 C++ 的版本(假定 f 接受的是一个指向 Foo 值的指针,h 返回一个整型数)。
呃,你还需要做一些事情,就是你该如何调用它:
1 2 3 4 5 6 |
|
在 C++ 中,事实上你可以得到相同的函数性,只是并非通过修改返回类型,而是通过抛出异常而已(看到这些 C++ 代码,现在你可以发出第一声惊呼了,“嘿,看起来像是单子!”)
如果我们的 Haskell 示例中一旦任何函数报错(抛出异常),compose 剩下的计算便会被忽略。你可以认为 C++ 异常要比 Maybe 单子更强大,这种认识没有错。但是要知道我还没有向你展示 Error 单子和 Exception 单子呢。
Haskell 的 Exception 单子胜出 C++ 异常之处在于类型检测。还记得向 C++ 类型系统添加异常规范的悲催经历么(Java 一样悲催)?C++ 标准如是说:
一个实现不应当因为一个表达式在被执行时抛出或者可能抛出一个不被这个实现所包含的函数允许的异常而拒绝它。
换句话说,C++ 的异常规范是善意的注释。Haskell 中却不是这样!如果一个函数返回一个 Maybe 或 Exception 值,它便编程类型签名的一部分,无论是在应用时还是在函数的定义时都会被检测。欺骗是行不通的,句号。
其实 Haskell 与 C++ 在异常处理方面最主要的区别是 do 表达式适用于所有单子,而 C++ 那个巧妙的 try/catch 语法只适用于异常。
阅读 Haskell 的单子代码时需要注意,虽然在用法上有些相似,但左向箭头并非赋值。左侧的标示符对应续延(也就是 do 块余下的部分)的参数值。它是右侧表达式所得结果解开后得到的值。这种解包行为总是在 bind 内部进行的。
非确定计算
前面,我曾通过定义函子与两个函数族的方式介绍过列表单子。这个函子的类型构造子部分可将任何类型 a 映射为 [a]。作用于函数的部分(现在我们知道了,这就是 fmap,不过对于列表而言它是 map)可将这个函数作用于列表中的每个元素。unit 与 join 都是多态函数,unit 被定义为:
1
|
|
join 函数就是 concat 函数。
现在我可以告诉你,列表单子提供了实现非确定计算的解决方案。想像一下,解析一个不确定的语法。对于相同的输入而言结果可能是多个候选解析树。
这些计算类型可以通过让函数返回可能结果的列表来模拟。我们可以故伎重演:一个非确定解析器所返回的任何结果(例如一个解析树类型),都会被转化为一个增强的类型(一个解析树列表)。
我们已经见识过列表单子的范畴论构造,但是这里我们面对的问题有些不同:如何将返回列表的函数串联起来。我们知道,这需要定义 bind 函数。它的签名在这种情况下是:
1
|
|
它接受一个列表(前一个函数的结果)和一个续延,(a -> [b]),结果必须要产生一个列表。续延显然是要作用于所输入列表中每一个元素的。但是优于续延也产生一个列表,我们最终得到的是列表的列表。为了得 到单层列表,只需消除子列表即可。基于此,bind 的实现如下:
1
|
|
续延作用于所输入列表中每个元素,是通过 map 来实现的。
我们可以使用 join 与 fmap 来定义 bind,这是巧合吗?肯定不是。单子的函子定义转换为 Klesisli 三元组有一个通用的公式:
接受函子的对象映射部分(类型构造子)。
定义 bind 函数:
bind x f = join ((fmap f) x)),其中 fmap 是函子的态射映射部分。将 unit 定义为 return
现在我们知道了如何在这两种定义之间进退了。
就像在 Maybe 的情况一样,我们可以对返回列表的函数应用 do 表达式:
1 2 3 4 |
|
其中 tossDie 返回一个骰子投掷后所有可能的结果构成的列表,toss2Dice 返回的是骰子投掷两次所得的所有结果的总和所构成的列表。
有趣的现象是列表单子与列表解析式的相关性。上面的例子等价于:
1
|
|
总结
很大一类计算都是以非函数式的方式将输入转化为输出。其中有许多可以表示为返回增强类型的结果的函数。结果的增强可采用类型构造子的形式表示。这种类型构造子定义了单子的第一个构成部分。
因为计算必须是可复合的,所以我们需要一种可以复合增强的函数的方式。这就引入了单子的第二个构成部分,即 bind 高阶函数族。
最后,我们需要构造可以返回增强类型的函数,为了解决这个问题,我们需要单子的第三个构成部分,return 函数族。它们可以将常规值转化为增强类型的相应的值。
第三部分
函数、状态与副作用
有这么一个问题:在函数式语言中,每次使用相同的参数值调用一个函数时,它必须要返回同样的结果。事实上,如果编译器检测到这样的情况,它会记住第 一次函数调用的返回结果,并忽略后续的调用。但是,对于依赖状态的计算,可能对于相同的参数值调用会每次返回不同的结果。例如程序要访问或修改一些全局或 静态变量,这就是带有“副作用”的函数。极端的情况下,有些计算可能就是为了副作用而被执行的,并不打算返回任何结果。
这种事情即便是在命令式编程中也是非常烦人的问题。全局变量的使用是特别不被推荐的。更好的解决方案是将状态封装起来,然后显式的传递给要使用它的 函数。在面向对象语言中,作为一种语法糖,部分状态可以作为隐含的“this”或“self”参数值传递给函数。甚至有一种语法可以将这样的函数复合起 来,像下面的 JavaScript 代码片段:
1 2 3 4 |
|
其中,title 与 write 分别是 document 对象的一个属性与一个方法(如果你带上单子眼镜的话,你看到的像是 do 语法块的一种东西)。
在函数式语言中,我们有更多的限制:我们不能够修改任何数据。有一种标准的方法克服这一限制:不要修改数据,而是要创建一个可修改的副本。如果语言 支持以引用来替代副本的智能数据结构的话,这样做甚至不需要付出太多代价。Haskell 中列表的大部分操作都是采用这种方式进行优化的。甚至有一种语言—Clojure 的整个核心都是基于“持久”的数据结构而构建的,这种数据结构看上去似乎不可被修改,实际上在后台却进行了大量的内存共享处理。在编写并行程序时,数据的 不可修改性(Immutability)是一项非常有诱人的特性:不需要同步即可访问不可修改的数据。
总而言之,将依赖于状态的计算翻译为函数式语言的方法就是使用可以显式接受状态(封装在某种数据结构中)并且返回可能被修改的状态以及常规返回值的函数。例如,下面这样的 C++ “函数”:
1 2 3 4 5 |
|
这个函数操作着一个类型为 std::vector 的全局向量 glob,将其翻译为 Haskell 函数:
1
|
|
这个 Haskell 函数操作着一个状态值,该值的类型为 Stack:
1
|
|
值构造子 ST 可从一个整型数值列表创建一个 Stack 类型的值。这个值构造子也可用于模式匹配,像 pop 函数的参数那样。head 函数返回列表的第一个元素,tail 函数返回去除了第一个元素的列表。
pop 函数的签名是典型的用于处理状态的函数签名:
1
|
|
这种类型的函数通常被称为“动作(Action)”。
对于这种模式的函数,存在两个问题:(1)它太丑了;(2)缺乏单子风格。上面的示例,采用 C++ 代码表示的原始的计算是不接受参数并返回一个整型数,而转化为函数式语言时则变成要接受一个状态值然后再返回一个整型值与状态值的复合值。现在还不清楚该 如何将这样的函数绑定起来并对它们应用方便的 do 语法。
我们正走在正确的道路上。现在只需要将视野再放宽一些:将动作的构建与执行隔离开来。这只需要构建一个函数,使其返回一个动作,这样的函数我们称之为“单子函数”。因为动作是一个函数,我们要处理的是返回函数的函数,即高阶函数。
我们的目标就是寻找一种方式,用于将一些单子函数复合为更大的单子函数。一个复合的单子函数可以返回一个复合的动作。然后基于一个状态执行这一动作,从而得到结果。
上述方式更加复合单子之道。我们可以从一个通用的状态计算开始,该计算接受一个类型为 a 的参数值,返回一个类型为 b 的参数值,我们要将其转化为一个单子函数,使得该函数接受类型 a 的值并返回一个以 b 为基础的增强类型的值,只不过这一次增强类型是函数类型——动作而已。一般情况下,一个动作是接受一个状态(类型为 S 的值)并返回一个由状态与类型 b 的值所构成的二元组的函数,其签名如下:
1
|
|
这就是状态单子的第一要素——类型构造子:对于任意类型 t,它定义了一种新的类型:对于给定的状态计算类型为 t 的值的一个动作。这种类型构造子是状态单子的一部分。在通往状态单子的正式定义之前,我们需要热热身。
单子计算器
基于状态的计算有一个完美的示例:一个基于状态的计算器。在该示例中,状态可表示为:
1
|
|
其中隐含了一个整型数值列表——计算器栈。
首先,我们定义一个单子函数(返回动作的函数),使之从计算器栈中弹出一个元素。这个是返回函数的函数,所以我们需要使用匿名函数来实现:
1 2 |
|
匿名函数几乎是上面 pop 函数的翻版。注意 popCalc 函数不接受任何参数,但是它返回一个可以接受一个计算器状态作为参数值然后返回这个计算器状态与计算结果(计算器栈顶端的值)打包的值。换句话 说,popCalc 返回的是一个承诺:一旦计算器栈可用之时,它便会返回栈顶的值。
使用 popCalc 的方法是:首先,调用它并记录其返回的动作;然后创建一个计算器状态(带有一个非空栈);继而将动作应用于计算器状态,对于所得结果可以使用模式匹配来获取最终用计算结果。具体过程如下:
1 2 3 4 5 |
|
下面我们采用同样的思想实现 pushCalc 函数:
1 2 |
|
注意 pushClac 所产生的匿名函数返回的是一个被修改了的计算器状态以及一个类型为 unit 的特殊的值 ()——void 的 Haskell 对等物——的打包结果。这个函数如果使用命令式语言来实现,只能返回 void 并且通过副作用的方式进行工作。还应当注意到这个匿名函数实际上是一个闭包:它捕获外部变量 n 留待后续使用。
最后,我们需要一个函数来执行一些计算,毕竟我们是要实现一个计算器。
1 2 3 4 |
|
其中我使用了模式 (a:b:rest) 来匹配计算器栈,以此来获取栈顶两个元素。被修改后的计算器状态,栈顶是原栈顶两个元素的和。
我们可以使用这些函数的复合来实现更为复杂的操作,例如将两个数相加。下面的代码跟 Rube Goldberg 机有一拼:
1 2 3 4 5 6 7 8 9 10 11 12 |
|
实际上我们真正想做的是将小的动作组合为大的动作。对于这个目的,我们需要定义 bind 函数,在这种情况下,其签名应该是:
1 2 3 |
|
这个签名看起来要比 Maybe 单子的 bind 函数的签名复杂的多,但是这仅仅是因为前者的增强类型其本身也是一个函数类型,其他方面则是相同的:bind 接受一个动作和一个续延,然后返回一个新动作。这种情况中的续延接受一个类型为 a 的参数值(要被第一个动作计算的值),然后返回一个复合的动作。
事实上,如果我们采用类型别名的形式定义动作:
1
|
|
那么 bind 函数的签名可以缩写为:
1
|
|
下面来看如何实现 bind。因为 bind 的结果是一个动作,那么它必须返回一个签名合适的匿名函数。
1 2 |
|
bind 是用于复合动作 act 与续延 cont 的,因此它应当首先对 clac 应用 act:
1
|
|
结果是一个元组 (clac’, v),其中 v 是类型为 a 的值,这正是续延所期望的参数值,因此紧接着就是应用续延:
1
|
|
续延的结果是一个新动作。这个新动作可以被执行,即应用于新的计算器状态
1
|
|
从而产生所期望的结果——类型为 (Clac, b) 的元组。
因此 bind 完整的代码是:
1 2 3 4 5 6 |
|
为了完善状态单子的构造,我们还需要定义 return 函数,其签名为:
1
|
|
该函数的实现是相当直观的。它接受值 v 然后返回一个可以返回这个值的承诺:
1
|
|
敏锐的读者可能会注意到这个 return 函数不依赖于类型 Calc 的什么特性的。对于任何表示状态的任何类型,它都可以工作。这样的话,我们就可以构造一个通用的状态单子了。基于状态的计算器就是这种单子的一个实例。
将 bind 函数采用中缀操作符的形式表示并不困难,将计算器状态转化 Haskell 编译器可以识别的单子也不困难。这样,add 函数的相关部分就可以写成 do 表达式的形式:
1 2 3 4 5 6 |
|
上述代码如果进行脱糖的话,就可以变成级联嵌套的匿名函数式:
1 2 3 4 5 6 |
|
你在 Haskell 程序中通常看不到这样的表达式,只不过我想超越 Haskell 的范畴。我的目标是能够将其与 C++ 联系起来,这种形式最方便进行语义转换。
因此我们不辞劳苦分析一下上面的代码。我们首先将第一个动作 (pushCalc x) 绑定到余下的代码。余下的代码是一个巨大的匿名函数。为了让这两部分匹配,他们的类型必须匹配。pushCalc 动作所生成的值是 void,因此其类型是 Action ()。因此它所绑定的匿名函数的类型也必须是接受 void 值的,其形式为:
1
|
|
匿名函数体是又是一个 bind,以此类推,直至到达我们最感兴趣的部分——popCalc。
popCalc 动作可以计算一个值:其签名为 Action Int。这个值被传入 popCalc 所绑定的那个匿名函数,因此最后的那个匿名函数会接受一个 Int 类型的参数值 z。最后这个值被 return 函数封装到一个动作中。
这种脱糖后的代码阐释了 Haskell 单子方法的全貌。Haskell 是一种惰性语言:只有最终目标真正需要的时候才会进行求值。还有,对于一些独立的事务进行求值时,它会以一种随意的次序进行。因此如果有可能实现 push 与 pop 的 Haskell 版本,我们会遇到两个问题:push 可能永远都不会被求值,因为它没有产生任何结果,甚至它可能会在 pop 之后被求值。单子的 bind 可以通过引入显式的数据依赖性强制动作的求值次序。如果在 bind 链中 pop 尾随着 push,那么 pop 不可能会先于 push 求值,因为它的参数值是 push 返回的计算器状态。它们两个被数据依赖性连接了起来,这种机制在 do 表达式中是不好看到的。
总结
从编程的视角来看,状态单子是非常有趣的一种模式。其意不在于处理什么,而在于创建一种可在后续中执行(甚至是可能多次执行)的动作。单子的框架提 供了一套设施,例如动作的复合机制以及可以让代码看起来更自然的 do 表达式。状态单子有一种有趣的变种,称为 IO 单子,在 Haskell 语言中它被用于处理输入与输出的任务。
命令式语言中有许多种模式或多或少的呈现出状态单子的形式。例如在 OO 世界中你可能会遇到非常有用的命令模式。你可以使用复合模式来 “绑定”命令对象。在那些支持匿名函数与闭包的语言中,例如 JavaScript、C# 以及最近的 C++,你可以直接从函数返回函数。这可能对于处理逆向控制会有帮助,这种逆向控制表现为:你返回了一个闭包并将其作为事件处理器(对于这个问题,我会再 写一系列博文)。
其实我考虑的一个非常特殊的例子是:我曾经使用 C++ 以完全贴合单子模式的方式编程。这篇文章之后我会写这个。
转载时,希望不要链接文中图片,另外请保留本文原始出处:http://garfileo.is-programmer.com
2012年9月01日 12:13
谢谢楼主的辛苦翻译,我是先知道英文版才看到你的博客的
我在看完中文版后,又看了一下原版,发现这里有一个可能翻译的不准确的地方,看中文的时候就有点疑惑.
Nondeterministic “functions”: They don’t return a single result but a choice of results.
非确定“函数”:它们不返回单个结果,而是返回多个可选的结果。
a choice of results应该是可能的结果中的一个吧,
而不是多个可选的结果,我还以为是返回多个值呢...
2012年9月02日 16:41
@LoveDavid:
我觉得还是“返回多个可选的结果”更贴切一些,因为函数的返回值是列表,是一个集合,它本来就是要包含零个、一个或多个值的。至于选择哪个值,那个函数管不着,而是由它的使用者来决定。
2012年9月03日 14:06
@LoveDavid: 有同感。个人觉得“不返回单一结果,而是在多个结果中选一个来返回”更加合适。
2012年12月26日 22:33
Endomorphism应该翻译成自同态更加准确,而不是自态射.
2013年2月21日 11:30
图全打不开了哦
2013年4月13日 16:14
@书痕: 因为那些图原先是在我的 github 空间里的,后来我把那个账户删了。可以看原文中的图。不过,我已经对 haskell 失爱好久 :)
2013年5月17日 15:13
@Garfileo: 是为什么失爱的呢?
2013年5月20日 17:54
@依云: 因为太抽象了。打算看一遍 sicp,学一下泛函分析,然后再回过头来,也许会对 haskell 再爱 :D
2013年5月20日 20:13
@rca: 啊,连名字都改了、博客又换了么?
2013年5月22日 22:02
@依云: 不小心露了行踪。。。