HELLO,遗传算法!
这篇文章讲述如何利用遗传算法解决一个二元函数的最大值求解问题。由于我对遗传算法的理解还处于菜鸟级别,所以本文所讲的方法以及所写的程序不一定 正确。之所以写这篇文章,是因为我已经烦透了教科书或论文里对遗传算法那么刻板的叙述,所以很想写一篇稍微轻松一点的入门文档,娱乐一下。
问题
这个二元函数是这样的:[tex]f(x,\,y)=0.5-\frac{\sin^2{\sqrt{x^2+y^2}-0.5}}{1+0.001(x^2+y^2))^2}[/tex]
要是我能够在脑袋 CPU 里生成这个函数的图像该有多好,可惜我不能够,所以用 gnuplot 画了一下,形貌如下图所示。
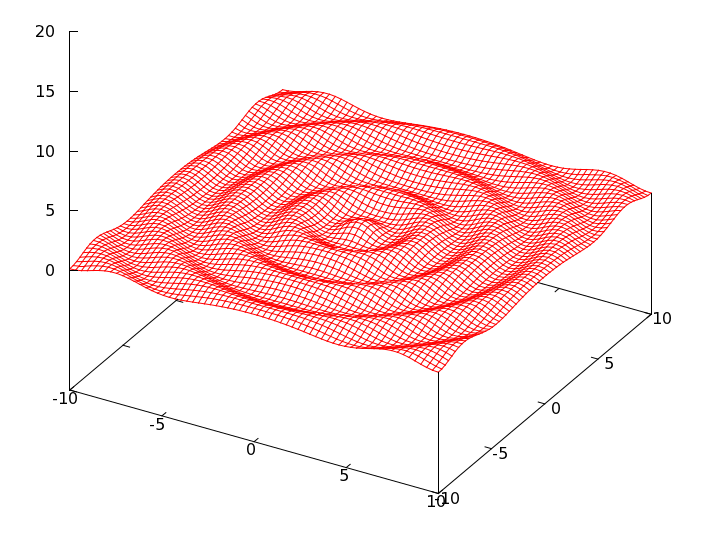
这 个函数看上去有点像是平静的池塘里丢了一颗小石子激起的波纹。我们的任务是计算这个函数在[tex]x\in [-10,\,10],\;y\in [-10,\,10][/tex] 范围之内的最大值。其实,这个函数在 [tex]x\in [-100,\,100],\;y\in [-100,\,100][/tex] 范围内所呈现的状态是波澜壮阔的,因为 gnuplot 的渲染能力有限,在此仅选取其一隅而绘制。
这个函数有无限个极大值,但是仅有一个最大值,位于 (0, 0) 点,值为 1。如果你的微积分学知识还没有遗忘,那么可以用数学方法进行求解一番。不幸的是,我已经忘光了,所以我只好用遗传算法进行求解。因为遗传算法的特点之一就是:不需要求导或其他辅助知识,而只需要影响一些可以影响搜索方向的目标函数和相应的适应度函数。所谓的目标函数,就是要求解的函数,也就是上述的那个函数。至于适应度函数,下文加以介绍。
创造染色体
我 唯一接触到生物学是在我的初中时代。就读的那个初中学校是一个落后的乡村中学,不过却拥有一个很好的教生物的老师,但是悲剧的是我在那时是一个不喜欢上课 的懵懂无知的顽童。现在为了理解遗传算法,我只好将“染色体”理解成一根带子,其上写着一组数据,据说这组数据记录着我们应该长成什么样子,具备什么样的 天赋,可能会生什么疾病等等。如果上帝能够将“语言程序”记录在我们的染色体中,也许我们刚生下来就可以说上百种人类语言还有火星语了。
虽然我们不是上帝,但是我们也可以创造染色体,例如 “000110001100” 或者 “000XXX00XXX0X”。这是一件很容易的事情,而真正困难的是如何在染色体中记录信息。因为用二进制来表示染色体比较方便程序计算,所以本文选择了这种最简单的方式。
现在,尝试为上文所述的函数 f(x, y) 的最大值所对应的 x 和 y 的值构造染色体。也就是说,要在一组二进制位中存储函数 f(x, y) 的定义域中的数值信息。
显 然,函数 f(x, y) 的定义域所包含的数值是无限多的,但是基于采样的办法可以得到有限集。例如,对于 [tex][-10,\,10][/tex] 这个区间,我们可以将它平均划分为 [tex]20\times 10^6[/tex] 个子区间,便得到精度为 8 位,小数位为 6 位的一组数值,个数为 [tex]20\times 10^6 + 1[/tex] 。若用一组二进制位形式的染色体来表示这个数值集合,那么我们还要考虑所用二进制位的长度。由于 [tex]2^{24}<20\times 10^6 + 1< 2^{25}[/tex],因此我们可以将染色体长度确定为 25 位,因为只有如此才可以让足够多的染色体表示那么多的数值,同时又不至于太浪费。虽然长度为 25 的二进制位所能表示的数值个数要多于 [tex]20\times 10^6 + 1[/tex],但是这并没有负面作用,相反,它可以更精确的表示区间 [tex][-10,\, 10][/tex] 中数值。
现在,我们已经创建了一种 25 位长度的二进制位类型的染色体,那么对于任意一个这样的染色体,我们如何将其复原为 [tex][-10,\,10][/tex] 这个区间中的数值呢?这个很简单,只需要使用下面的公式即可:
[tex]f(c) = -10.0 + c\cdot\frac{10.0 - (-10.0)}{2^{25} - 1}[/tex]
例 如 0000 0000 0000 0000 0000 0000 0000 0 和 1111 1111 1111 1111 1111 1111 1 这两个二进制数,将其化为 10 进制数,代入上式,可得 -10.0 和 10.0。这意味着长度为 25 位的二进制数总是可以通过上式转化为 [tex][-10,\,10][/tex] 区间中的数。
个体、种群与进化
染色体表达了某种特征,这种特征的载体,可以称为“个体”。例如,我本人就是一个“个体”,我身上载有 23 对染色体,也许我的相貌、性别、性格等因素主要取决于它们。众多个体便构成“种群”。
对 于本文所要解决的二元函数最大值求解问题,个体可采用上一节所构造的染色体表示,并且数量为 2 个,其含义可理解为函数 f(x, y) 定义域内的一个点的坐标。许多这样的个体便构成了一个种群,其含义为一个二维点集,包含于对角定点为 (-10.0, -10.0) 和 (10.0, 10.0) 的正方形区域。
也许有这样一个种群,它所包含的个体对应的函数值会比其他个体更接近于函数 f(x, y) 的理论最大值,但是它一开始的时候可能并不比其他个体优秀,它之所以优秀是因为它选择了不断的进化,每一次的进化都要尽量保留种群中的优秀个体,淘汰掉不 理想的个体,并且在优秀个体之间进行染色体交叉,有些个体还可能出现变异。种群的每一次进化后,必定会产生一个最优秀的个体。种群所有世代中的那个最优个 体也许就是函数 f(x, y) 的最大值对应的定义域中的点。如果种群不休止的进化,它总是能够找到最好的解。但是,由于我们的时间是有限的,有可能等不及种群的最优进化结果,通常是在 得到了一个看上去还不错的解时,便终止了种群的进化。
那么,对于一个给定的种群,我们如何赋予它进化的能力呢?
- 首先是选择。对于种群的每一代个体,可以用一个适应度函数(也叫评估函数)计算个体的适应度,根据适应度可以计算出个体的生存几率。适应度较大的个体被保留的可能性也较大,反之被淘汰的可能性较大。
- 其次是交叉,在一定的概率下对两个个体的染色体进行交叉重组,从而得到两个新个体。
- 最后是变异。即有些个体的染色体会以一定的概率发生变化。
达 尔文的进化论也许并不正确,但是它对于我们运用这种理论来计算问题并没有什么错误的影响。我们不管人类是否是由猿猴进化来的,还是由别的什么生物。那些进 化论的反对者总是想用自己的理论推翻进化论,不过他们的理论连人类是什么进化来的都搞不清楚,只好说人类是天外来客或者是上帝创造的。当然,我也不反对上 帝创造了人类,那么上帝也许用的是遗传算法,所以达尔文又一次正确了。基督徒们相信世界末日,也许只是因为上帝的时间也有限,等不及人类进化到最优解,于 是上帝就设定了人类进化的最大世代数。
种群的设计
如果你不熟悉 python 语言,那么请原谅我使用了它。
import math, random
class Population:
def __init__ (self, size, chrom_size, cp, mp, gen_max):
# 种群信息
self.individuals = [] # 个体集合
self.fitness = [] # 个体适应度集合
self.selector_probability = [] # 个体选择概率集合
self.new_individuals = [] # 新一代个体集合
self.elitist = {'chromosome':[0, 0], 'fitness':0, 'age':0} # 最佳个体的信息
self.size = size # 种群所包含的个体数
self.chromosome_size = chrom_size # 个体的染色体长度
self.crossover_probability = cp # 个体之间的交叉概率
self.mutation_probability = mp # 个体之间的变异概率
self.generation_max = gen_max # 种群进化的最大世代数
self.age = 0 # 种群当前所处世代
# 随机产生初始个体集,并将新一代个体、适应度、选择概率等集合以 0 值进行初始化
v = 2 ** self.chromosome_size - 1
for i in range (self.size):
self.individuals.append ([random.randint (0, v), random.randint (0, v)])
self.new_individuals.append ([0, 0])
self.fitness.append (0)
self.selector_probability.append (0)
基于轮盘赌博机的选择
我们可以将物竞天择简单化,将种群的各个个体摆在一个轮盘上,然后转一下轮盘,将盘外的指针所指向的个体保留下来,然后接着转轮盘,接着选择,直至产生一组与种群原有个体数量一致的个体,这就是我们所选择的下一代,虽然他们坚持赌博是违法的。
要模拟这个轮盘赌博机制,首先需要构造个体适应度评价机制:
# 接上面的代码
def decode (self, interval, chromosome):
d = interval[1] - interval[0]
n = float (2 ** self.chromosome_size -1)
return (interval[0] + chromosome * d / n)
def fitness_func (self, chrom1, chrom2):
interval = [-10.0, 10.0]
(x, y) = (self.decode (interval, chrom1),
self.decode (interval, chrom2))
n = lambda x, y: math.sin (math.sqrt (x*x + y*y)) ** 2 - 0.5
d = lambda x, y: (1 + 0.001 * (x*x + y*y)) ** 2
func = lambda x, y: 0.5 - n (x, y)/d (x, y)
return func (x, y)
def evaluate (self):
sp = self.selector_probability
for i in range (self.size):
self.fitness[i] = self.fitness_func (self.individuals[i][0],
self.individuals[i][1])
ft_sum = sum (self.fitness)
for i in range (self.size):
sp[i] = self.fitness[i] / float (ft_sum)
for i in range (1, self.size):
sp[i] = sp[i] + sp[i-1]
decode 函数可以将一个染色体 chromosome 映射为区间 interval 之内的数值。fitness_func 是适应度函数,可以根据个体的两个染色体计算出该个体的适应度,这里直接采用了本文所要求解的目标函数:
[tex]f(x,\,y)=0.5-\frac{\sin^2{\sqrt{x^2+y^2}-0.5}}{1+0.001(x^2+y^2))^2}[/tex]
作为适应度函数。
evaluate 函数用于评估种群中的个体集合 self.individuals 中各个个体的适应度,即将各个个体的 2 个染色体代入 fitness_func 函数,并将计算结果保存在 self.fitness 列表中,然后将 self.fitness 中的各个个体适应度除以所有个体适应度之和,得到各个个体的生存概率。为了适合轮盘赌博游戏,需要将个体的生存概率进行叠加,从而计算出各个个体的选择概 率。
例如有 5 个个体,其适应度与选择概率为:
| 个体 | 适应度 | 生存概率 | 选择概率 |
|---|---|---|---|
| 1 | 0.9042845033795694 | 0.28693981857759787 | 0.28693981857759787 |
| 2 | 0.5588628304907922 | 0.17733356990137467 | 0.46427338847897254 |
| 3 | 0.6899948769706024 | 0.21894326849291637 | 0.6832166569718889 |
| 4 | 0.3114709778723004 | 0.09883330472749545 | 0.7820499616993843 |
| 5 | 0.6868647339474463 | 0.21795003830061557 | 0.9999999999999999 |
有了这些数据,便可以构造类似下图所示的轮盘赌博机了。

这个轮盘赌博机,使用用 python 语言可以表示为:
# 接上面的代码
def select (self):
(t, i) = (random.random (), 0)
for p in self.selector_probability:
if p > t:
break
i = i + 1
return i
染色体交叉模拟
# 接上面的代码
def cross (self, chrom1, chrom2):
p = random.random ()
n = 2 ** self.chromosome_size -1
if chrom1 != chrom2 and p < self.crossover_probability:
t = random.randint (1, self.chromosome_size - 1)
mask = n << t
(r1, r2) = (chrom1 & mask, chrom2 & mask)
mask = n >> (self.chromosome_size - t)
(l1, l2) = (chrom1 & mask, chrom2 & mask)
(chrom1, chrom2) = (r1 + l2, r2 + l1)
return (chrom1, chrom2)
cross 函数可以将两个染色体进行交叉配对,从而生成 2 个新染色体。
此 处使用染色体交叉方法很简单,先生成一个随机概率 p,如果两个待交叉的染色体不同并且 p 小于种群个体之间的交叉概率 self.crossover_probability,那么就在 [tex][0, \text{self.chromosome\_size}][/tex] 中间随机选取一个位置,将两个染色体分别断为 2 截,然后彼此交换一下。例如:
1000 1101 1100 0010 0001 0110 1
0001 0011 1111 1001 0010 1110 0
在第 10 位处交叉,结果为:
1000 1101 1100 0011 0010 1110 0
0001 0011 1111 1000 0001 0110 1
这种染色体交叉方法叫做“单点交叉”。如果不嫌麻烦,也可以使用多点交叉。
染色体变异模拟
# 接上面代码
def mutate (self, chrom):
p = random.random ()
if p < self.mutation_probability:
t = random.randint (1, self.chromosome_size)
mask1 = 1 << (t - 1)
mask2 = chrom & mask1
if mask2 > 0:
chrom = chrom & (~mask2)
else:
chrom = chrom ^ mask1
return chrom
mutate 函数可以将一个染色体按照变异概率进行单点变异。例如:
1000 1101 1100 0010 0001 0110 1
在第 13 位发生变异,结果为:
1000 1101 1100 1010 0001 0110 1
同交叉类似,也可以进行多点变异。
进化过程
# 接上面的代码
def evolve (self):
indvs = self.individuals
new_indvs = self.new_individuals
# 计算适应度及选择概率
self.evaluate ()
# 进化操作
i = 0
while True:
# 选择两个个体,进行交叉与变异,产生新的种群
idv1 = self.select ()
idv2 = self.select ()
# 交叉
(idv1_x, idv1_y) = (indvs[idv1][0], indvs[idv1][1])
(idv2_x, idv2_y) = (indvs[idv2][0], indvs[idv2][1])
(idv1_x, idv2_x) = self.cross (idv1_x, idv2_x)
(idv1_y, idv2_y) = self.cross (idv1_y, idv2_y)
# 变异
(idv1_x, idv1_y) = (self.mutate (idv1_x), self.mutate (idv1_y))
(idv2_x, idv2_y) = (self.mutate (idv2_x), self.mutate (idv2_y))
(new_indvs[i][0], new_indvs[i][1]) = (idv1_x, idv1_y)
(new_indvs[i+1][0], new_indvs[i+1][1]) = (idv2_x, idv2_y)
# 判断进化过程是否结束
i = i + 2
if i >= self.size:
break
# 更新换代
for i in range (self.size):
self.individuals[i][0] = self.new_individuals[i][0]
self.individuals[i][1] = self.new_individuals[i][1]
evolve 函数可以实现种群的一代进化计算,计算过程分为三个步骤:
- 使用 evaluate 函数评估当前种群的适应度,并计算各个体的选择概率。
- 对 于数量为 self.size 的 self.individuals 集合,循环 self.size / 2 次,每次从 self.individuals 中选出 2 个个体,对其进行交叉和变异操作,并将计算结果保存于新的个体集合 self.new_individuals 中。
- 用种群进化生成的新个体集合 self.new_individuals 替换当前个体集合。
如果循环调用 evolve 函数,那么便可以产生一个种群进化的过程,如下:
# 接上面的代码
def run (self):
for i in range (self.generation_max):
self.evolve ()
print (i, max (self.fitness), sum (self.fitness)/self.size,
min (self.fitness))
run 函数根据种群最大进化世代数设定了一个循环。在循环过程中,调用 evolve 函数进行种群进化计算,并输出种群的每一代的个体适应度最大值、平均值和最小值。
扮演一次上帝
下面的代码可以执行上述的种群进化过程:
# 接上面的代码
if __name__ == '__main__':
# 种群的个体数量为 50,染色体长度为 25,交叉概率为 0.8,变异概率为 0.1,进化最大世代数为 150
pop = Population (50, 24, 0.8, 0.1, 150)
pop.run ()
注意,因为个体交叉的需求,种群所包含的个体数量一般设为偶数。本文的程序没考虑个体数量为奇数的情况。
如果将以上所有出现的 python 代码依序组装在一起,假设存为 test.py 文件,那么执行下面的命令便可运行这个脚本:
$ python3 test.py
注意,这里我们使用的是 python 3。如果你的系统中只安装了 python 2,那么只需在 test.py 的首行添加:
# -*- coding: utf-8 -*-
然后将 evolve 函数中的 print 语句修改为:
print i, max (self.fitness), sum (self.fitness)/self.size, min (self.fitness)
这样便可以正确运行这个脚本了。
计算结果
如果使用命令:
$ python3 test.py > test.log
那么使用下面的 gnuplot 脚本 test.gnu 可以绘制出种群的每一代最大适应度、平均适应度和最小适应度的变化情况。
#!/usr/bin/gnuplot
set term pngcairo
set size ratio 0.75
set output 'test.png'
plot "test.log" using 1:2 title "max" with lines, \
"test.log" using 1:3 title "ave" with lines, \
"test.log" using 1:4 title "min" with lines
运行这个 gnuplot 脚本:
chmod +x ./test.gnu ./test.gnu
可以得到 test.png 文件,结果大致是下面这个样子。
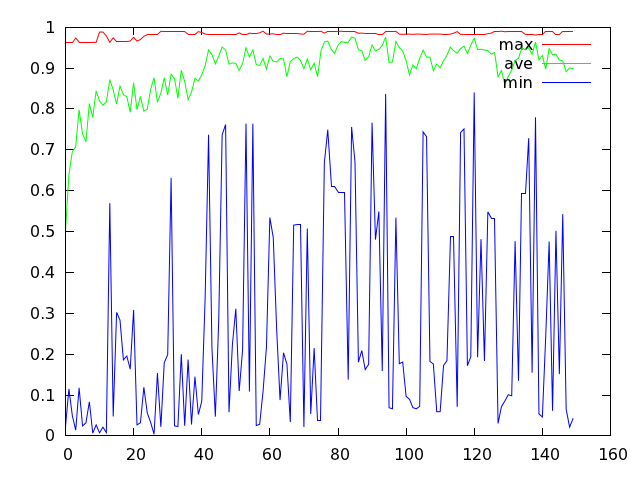
本 文所求解函数 [tex]f(x,\,y)=0.5-\frac{\sin^2{\sqrt{x^2+y^2}-0.5}}{1+0.001(x^2+y^2))^2}[/tex] 理论上的最大值为 1.0,而上图中红色的折线表示种群每一代个体中适应度最大值的变化情况,显然,我们所得结果是比较接近 1.0 的。
蓝色折线反映了种群每一代最差个体适应度的变动情况,它的波动幅度看上去比较剧烈。如果将变异概率设为 0.4,那么它看起来就会比较温顺一些:
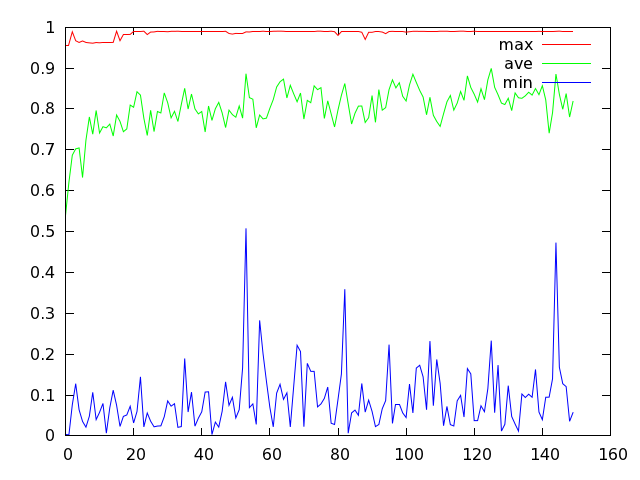
而且,变异概率如果设置的越大,那么蓝色折线的波动幅度便会越小。下图显示了比较极端的情况,此时变异概率设为 1.0。
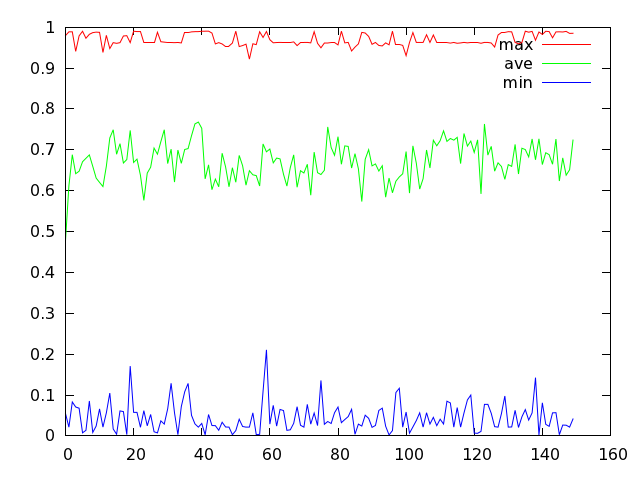
在固定变异概率的条件下,可以用类似的方法观察一下交叉概率对计算结果的影响。
几个定理
定理 1:标准遗传算法不能收敛至全局最优解。
本文程序是按照标准遗传算法实现的,从上面的几幅图也可以看出来,受交叉与变异的影响,种群的每一代个体的最大适应度都有可能在不断变化。
定理 2:标准遗传算法,如果在选择之前保留当前最佳个体,最终能收敛到全局最优解。
根据定理 2,对于本文所实现的遗传算法,只需要添加一个可以复制当前最佳个体信息的函数,即可保证全局最优解的收敛性,如下:
# 将该函数插入 Population 类中
def reproduct_elitist (self):
# 与当前种群进行适应度比较,更新最佳个体
j = 0
for i in range (self.size):
if self.elitist['fitness'] < self.fitness[i]:
j = i
self.elitist['fitness'] = self.fitness[i]
if (j > 0):
self.elitist['chromosome'][0] = self.individuals[j][0]
self.elitist['chromosome'][1] = self.individuals[j][1]
self.elitist['age'] = self.age
然后在 evlove 函数中调用 reporduct_elitist 函数:
# 修改后的 evolve 函数
def evolve (self):
indvs = self.individuals
new_indvs = self.new_individuals
# 计算适应度及选择概率
self.evaluate ()
# 进化操作
i = 0
while True:
# 选择两个个体,进行交叉与变异,产生新的种群
idv1 = self.select ()
idv2 = self.select ()
# 交叉
(idv1_x, idv1_y) = (indvs[idv1][0], indvs[idv1][1])
(idv2_x, idv2_y) = (indvs[idv2][0], indvs[idv2][1])
(idv1_x, idv2_x) = self.cross (idv1_x, idv2_x)
(idv1_y, idv2_y) = self.cross (idv1_y, idv2_y)
# 变异
(idv1_x, idv1_y) = (self.mutate (idv1_x), self.mutate (idv1_y))
(idv2_x, idv2_y) = (self.mutate (idv2_x), self.mutate (idv2_y))
(new_indvs[i][0], new_indvs[i][1]) = (idv1_x, idv1_y)
(new_indvs[i+1][0], new_indvs[i+1][1]) = (idv2_x, idv2_y)
# 判断进化过程是否结束
i = i + 2
if i >= self.size:
break
# 最佳个体保留
self.reproduct_elitist ()
# 更新换代
for i in range (self.size):
self.individuals[i][0] = self.new_individuals[i][0]
self.individuals[i][1] = self.new_individuals[i][1]
注 意,我没有将最佳个体保存在种群的个体集合中,因为我觉得一个既不参与交叉也不参与变异的个体,是不能放在种群中的,它应当存放在历史课本里。所以,我在 Population 类中设置了一个 elitist 的成员,用以记录最佳个体对应的染色体、适应度及其出现的年代。当遗传算法结束后,这个最佳个体可作为目标函数的解。
定理 3:遗传算法所接受的参数有种群规模、适应度函数、染色体的表示、交叉概率、变异概率等,对于这些参数而言,不存在一个最佳组合,使它对于任何问题都能达到最优性能。
也就是说,成功的设计一个遗传算法的关键在于针对具体问题去选择恰当的参数。如果不利用所求解一些问题的特定知识,那么算法的性能于我们采用何种参数没有多大关系,情况可能会更糟糕。还要记住的是,对于单个问题,不存在最好的搜索算法。
程序
本文完整的 python 程序可在这里下载
转载时,希望不要链接文中图片,另外请保留本文原始出处:http://garfileo.is-programmer.com
2011年2月19日 21:32
好熟悉的流程。
上学的时侯,没少背诵这些东西,可惜当时学的太理论化了,自己都没有试过,只是死记硬背了流程和一堆公式。
2011年2月19日 22:36
那个 reproduct_elitist 函数有问题,应该将 j 的初始值设为 -1,并将 '
if(j > 0)' 修改为 'if (j >= 0)'。